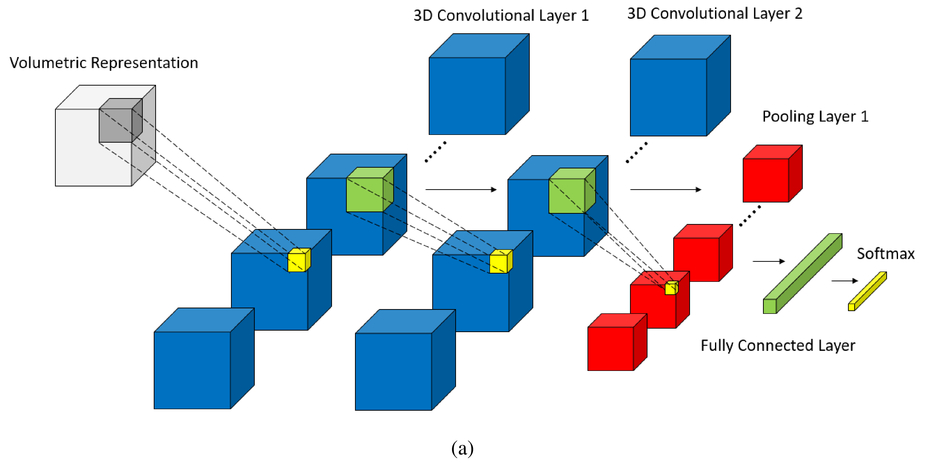
In this project we automate learning CNN hyper-params. We test and improve my previous tensorflow implementation of CNN in here on Kaggle's facial expression dataset. Here I only deal with two label classes: Happy and Angry. Randomized Search for learning hyper_paramters such as learning_rate, momentum coefficient, etc and drop-out regularizer improved the default test prediction accuracy from 36% to 64%. This is a bit lower than 72% that we got from our SVM classifier. However, we will continue in following projects to see if we can beat SVM modifying CNN architecture itself.
from utils import *
from classes import *
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import tensorflow as tf
from sklearn.grid_search import RandomizedSearchCV
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,confusion_matrix
%matplotlib inlineLoad data and observe label distribution
filename = "fer2013/fer2013.csv";
df = pd.read_csv(filename)
print(df.head())
sns.countplot(x='emotion',data=df) emotion pixels Usage
0 0 70 80 82 72 58 58 60 63 54 58 60 48 89 115 121... Training
1 0 151 150 147 155 148 133 111 140 170 174 182 15... Training
2 2 231 212 156 164 174 138 161 173 182 200 106 38... Training
3 4 24 32 36 30 32 23 19 20 30 41 21 22 32 34 21 1... Training
4 6 4 0 0 0 0 0 0 0 0 0 0 0 3 15 23 28 48 50 58 84... Training
<matplotlib.axes._subplots.AxesSubplot at 0x7fb52f519b50>
We start out with applying CNN on two class labels:0 (Angry) and 3 (Happy)
binary = True #read labels 3 and 4 only
balance = False
if binary:
df = df[(df['emotion']==3) | (df['emotion']==0)]
df['emotion'] = df['emotion'].apply(lambda x: 0 if x == 0 else 1)
X = df['pixels']
y = df['emotion']
if balance:
X, y = balanceClasses(X,y)
sns.countplot(x=y)<matplotlib.axes._subplots.AxesSubplot at 0x7fb52bc24610>
The parseCNNInput takes (N,k) array and converts it into (N,c,sqrt(k),sqrt(k)) matrix for CNN. In this process, the pixel values are scaled to 0-1.
X,y = parseCNNInput(X,y)Now we train a vanilla CNN with one 1 hidden layer and 2 pooling layers with default learning params
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
model = CNN(architecture_params=
{'pool_layer_sizes':[(20,5,5),(20,5,5)],
'hidden_layer_sizes':[500,300]
},
hyper_params={'lr':0.1, 'mu':0.9, 'reg':0.01, 'decay':0.99, 'eps':0.0001}
)model.fit(X_train,y_train,batch_sz=30,epochs=3,debug=True)
pred = model.predict(X_test)
err = error_rate(pred,y_test)
print("test error: " + str(err))
print(confusion_matrix(y_test, pred))
print("\n")
print(classification_report(y_test,pred))'\npred = model.predict(X_test)\nerr = error_rate(pred,y_test)\nprint("test error: " + str(err))\nprint(confusion_matrix(y_test, pred))\nprint("\n")\nprint(classification_report(y_test,pred))\n'
Lack of convergence shows that our parameter settings are not fine tuned. Lets learn the hyper paramters for this architecture. This includes learning_rate, momentum coefficient, regularizer parameter (l2), decay rate and epsilon. The way we will do this is to utilize scikit-learns Randomized Search to learn best paramters from 5D parameter space. Another way to do this would be is to use GridSearchCV which is an exhaustive search technique and would require long time to complete.
We needed to make some modifications to the vanilla-cnn code to add get_params,set_params, score method. The estimator would fit the input data on the result (error_rate) of 1 epoch of learning which should be a good estimatore for the parameters we are seeking.
The randomized search took around 20 mins on Alienware R313. Its good to run it couple of times and take the average parameter values.
#Using Randomized Search for searching optimal learning parameters
param_grid = {'lr':[0.00001,0.0005, 0.0001, 0.005, 0.001],'mu':[0.999,0.9945,0.99,0.945,0.9],'reg':[0.00001,0.00005,0.0001,0.0005,0.001],'decay':[0.999999,0.9999945,0.99999,0.999945,0.9999],'eps':[0.0001,0.0005,0.001,0.005,0.01]}
estimator = RandomizedSearchCV(CNN(architecture_params={'pool_layer_sizes':[(20,5,5),(20,5,5)],'hidden_layer_sizes':[500,300]}),param_grid, verbose=2)estimator.fit(X_train,y_train)Fitting 3 folds for each of 10 candidates, totalling 30 fits
('\nerror_rate: ', 0.347, ', params: ', {'mu': 0.999, 'eps': 0.01, 'lr': 1e-05, 'reg': 0.0001, 'decay': 0.999945})
[CV] mu=0.999, decay=0.999945, lr=1e-05, reg=0.0001, eps=0.01 - 13.1s
:
(Debug Output removed due to large size)
:
('\nerror_rate: ', 0.352, ', params: ', {'mu': 0.9945, 'eps': 0.0001, 'lr': 0.001, 'reg': 0.0001, 'decay': 0.999999})
[CV] mu=0.9945, decay=0.999999, lr=0.001, reg=0.0001, eps=0.0001 - 17.5s
[Parallel(n_jobs=1)]: Done 30 out of 30 | elapsed: 7.5min finished
print(estimator.best_params_){'mu': 0.945, 'decay': 0.9999945, 'lr': 0.0005, 'reg': 0.0005, 'eps': 0.001}
Utilizing the resulting best paramters of Randomized Search:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
model = CNN(architecture_params=
{'pool_layer_sizes':[(20,5,5),(20,5,5)],
'hidden_layer_sizes':[500,300]
},
hyper_params={'mu': 0.945, 'decay': 0.9999945, 'lr': 0.0005, 'reg': 0.0005, 'eps': 0.001}
)model.fit(X_train,y_train,batch_sz=30, epochs=6,debug=True)('\nerror_rate: ', 0.231, ', params: ', {'mu': 0.945, 'eps': 0.001, 'lr': 0.0005, 'reg': 0.0005, 'decay': 0.9999945})
pred = model.predict(X_test)
err = error_rate(pred,y_test)
print("test error: " + str(err))
print(confusion_matrix(y_test, pred))
print("\n")
print(classification_report(y_test,pred))test error: 0.6461097167443528
[[ 987 0]
[1802 0]]
precision recall f1-score support
0 0.35 1.00 0.52 987
1 0.00 0.00 0.00 1802
avg / total 0.13 0.35 0.19 2789
/home/mbastola/.local/lib/python2.7/site-packages/sklearn/metrics/classification.py:1135: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples.
'precision', 'predicted', average, warn_for)
This CNN architecutre showed ~24% in training validation error while ~64% test error! It seems like the cnn is overfitting on the input data. One way to try better this result is to utilize dropouts. We modified the vanilla cnn to include dropouts as input and in fit function. Finally, I use p = 0.2 dropout for input layer while 0.5 drop-out for hidden layers.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=42)
model_with_dropout_reg = CNN(architecture_params=
{'pool_layer_sizes':[(20,5,5),(20,5,5)],
'hidden_layer_sizes':[500,300],
'dropout_rates':[0.8, 0.5, 0.5]
},
hyper_params= {'mu': 0.945, 'decay': 0.9999945, 'lr': 0.0005, 'reg': 0.0005, 'eps': 0.001}
)model_with_dropout_reg.fit(X_train,y_train,batch_sz=30,epochs=6,debug=True)('\nerror_rate: ', 0.317, ', params: ', {'mu': 0.945, 'eps': 0.001, 'lr': 0.0005, 'reg': 0.0005, 'decay': 0.9999945})
pred = model_with_dropout_reg.predict(X_test)
err = error_rate(pred,y_test)
print("test error: " + str(err))
print(confusion_matrix(y_test, pred))
print("\n")
print(classification_report(y_test,pred))test error: 0.36428827536751524
[[ 71 916]
[ 100 1702]]
precision recall f1-score support
0 0.42 0.07 0.12 987
1 0.65 0.94 0.77 1802
avg / total 0.57 0.64 0.54 2789
We can see that adding dropout increased the training-validation error to ~31% but significantly reduced the testing error while ~36% test error, which is train_validation_error ~ test_error and a good state to be.